代数数据类型（ADT）的基本定义和演算

在充分简化且不考虑 bottom（Haskell 中的 undefined）的情况下 [6]，类型可以看作是值的集合，而集合包含的元素的数量，即集合的势，对应了类型可能的值的数量。下文把这个数量称作类型的大小。

以下是一些基本的定义。

data Void
data Unit = Unit
data Prod a b = Pair a b
data Sum a b = InL a | InR b
data Exp b a = Fun (a -> b)

Void [10] 是不含任何值的类型，大小为 0，在 C–H 同构 [7] [12] 中对应了假命题 [13]。

Unit 是只含一个值的类型，大小为 1。可以用作仅产生副作用的表达式的返回值类型，表示返回值不携带有意义的信息。另外，C 语言中以 void 作为函数返回类型时，void 其实更接近 Unit [11]。

Prod 和 Sum 产生积类型（Product Type）与和类型（Sum Type），对应了集合的笛卡尔积（Cartesian Product）[14] 和不交并（Disjoint Union，有时亦称 Tagged Union）[15]。在实际编程，比如 Haskell 中，积类型典型的例子就是 Tuple，和类型则是 Maybe。说到了 Maybe 就往往会顺带提一下 Null Reference 这个 Billion-dollar Mistake [17]，引入 Sum Type 或者像 Java 一样提供 Optional 这种 Maybe 类似物是可行的解决方案之一 [16]。

函数类型比较特别，对应的集合大小是指数形式的。首先在此处只考虑 total function 并且用外延等价来判断函数相等性，大小为 a 的参数类型 A 的每个可能的值，都存在且仅存在一个大小为 b 的返回类型 B 的值与之对应，那么类型为 A -> B 的函数就有 {$b^a$} 个 [8]。一个有趣的现象是，Void -> a 这个奇怪的函数类型存在且仅存在一个值，因为任何数的零次幂都等于一。这个类型在 C–H 同构下的意义是假命题可以推出任何命题，而那个唯一的值就是著名的 absurd 函数 [10] [18]。

在 [1]，[4] 和 [5] 中都提到了 ADT 生成了一个半环（semiring）。

容易得出一些基本类型的定义方法，比如 Bool，能取 True 或 False 两个值中的任意一个，记作 {$\text{Bool} = 1 + 1 = 2$}。

-- data Bool = False | True
type Bool = Sum Unit Unit

比如 Maybe a，要么是 Nothing，要么是 Just a，记作 {$\text{Maybe}(a) = 1 + a$}。

-- data Maybe a = Nothing | Just a
type Maybe a = Sum Unit a

再比如一个 Bool 和 Unit 的序对，记作 {$\text{T} = 2 \times 1 = 2$}。这个类型与 Bool 是同构的。

-- data T = T Bool Unit
type T = Prod Bool Unit

一个关于同构的笑话。

在 [1] 中对简单类型的同构的判断和具体的运算法则有详细介绍。

如果是递归定义的 ADT 呢？比如 List。

data List t = Nil | Cons t (List t)

这是经典的 List 定义，用前边定义的一系列 ADT 操作在理论上来讲也应该可以写成这样。

type List t = Sum Unit (Prod t (List t))

然而在 [1] 中提到了用 Haskell 的类型别名（Type Synonymous）写不出这样的类型，因为type 必须在做 type checking 前就被完全展开，然而 List 的展开是无穷无尽的，所以 [1] 中用了 newtype。

newtype List a = L (Sum Unit (Prod a (List a))

其实一定要用 type 写是可以的，但需要引入类型层面的不动点组合子。

newtype Fix d = Fix (d (Fix d))

以及对类型构造器的组合，因为类型别名虽然允许多参数，但并没有产生实际的类型构造器，所以试图通过把部分应用的类型别名传给 Fix 的写法会导致报错。

newtype Comp f g x = Comp (f (g x))

然后就可以写出类型别名，相关的值构造器（伪）和一个值。

type ListGen t = Comp (Sum Unit) (Prod t)
type List t = Fix (ListGen t)

cons :: t -> List t -> List t
cons x = Fix . Comp . InR . Pair x

nil :: List t
nil = Fix . Comp . InL $ Unit

x :: List Int
x = cons 1 $ cons 0 nil

回到最初的定义上来。

data List t = Nil | Cons t (List t)

省去转换到 Sum 和 Prod 的组合的步骤，这可以记作 {$\text{List}(a) = 1 + a \times \text{List}(a)$}，代换一下就变成了 {$\text{List}(a) = 1 / (1 - a)$}。然而之前并没有提到过 ADT 的减法和除法，而且似乎减法和除法也很难有实际的意义。此时我们可以做的是对 {$\text{List}(a)$} 进行（麦克劳林）级数展开，得到 [3]：

\[\text{List}(a) = 1 + a + a^2 + a^3 + a^4 + \dots\]

而这可以解读成，一个包含类型为 {$a$} 的值的列表，可以是空列表，可以包含一个 {$a$} 类型值，可以包含两个 {$a$} 类型值，可以包含三个 {$a$} 类型值……boom！

同样的结果也可以通过直接展开 {$\text{List}(a)$} 的定义得到，即：

\[\text{List}(a) = 1 + a \times \text{List}(a) = 1 + a \times (1 + a \times \text{List}(a)) = 1 + a \times (1 + a \times (1 + a \times \text{List}(a))) = \dots\]

再来看复杂一点的类型，比如二叉树。

data Tree a = Empty | Node a (Tree a) (Tree a)

记作 {$\text{Tree}(a) = 1 + a \times \text{Tree}(a) \times \text{Tree}(a)$}。把定义写成方程 {$a \times \text{Tree}(a)^2 - \text{Tree}(a) + 1 = 0$}，然后尝试解出 {$\text{Tree}(a)$}，结果是：

\[a = 0, \text{Tree}(a) = 1\] \[a \neq 0, \text{Tree}(a)_1 = \frac{1 - \sqrt{1 - 4 \times a}}{2 \times a}, \text{Tree}(a)_2 = \frac{1 + \sqrt{1 - 4 \times a}}{2 \times a}\]

如果 {$a$} 是 Void，那这个类型就只剩 Empty 可以存在了，所以 {$a = 0$} 的情况很合理。

{$a \neq 0$} 时的情况就比较麻烦了，这个方程有两个解，先看第一个 {$\text{Tree}(a)_1$}，它的麦克劳林展开是：

\[\text{Tree}(a)_1 = 1 + a + 2 \times a^2 + 5 \times a^3 + 14 \times a^4 + \dots\]

相比起 {$\text{List}(a)$} 的级数展开，这个式子里出现了一些常系数。{$1$} 是空树，{$a$} 是只有一个节点的树，{$2 \times a^2$} 说明了有两个节点的二叉树有两种不同的构型，{$5 \times a^3$} 说明了有三个节点的二叉树有五种不同的构型……事实上 {$1, 1, 2, 5, 14, \dots$} 这个序列有个名字叫做 Catalan Numbers，名称来自比利时数学家 Eugène Charles Catalan，而 The 18th century Chinese discovery of the Catalan numbers 一文则指出最早的对 Catalan Numbers 的使用见于清代数学家明安图的《割圜密率捷法》。

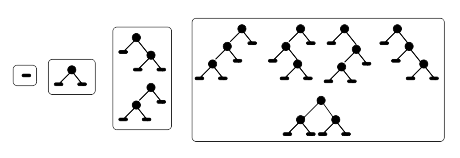
binary_tree

上图是在各种地方被用了很多次的不同节点数的二叉树的构型。 [19]

而对于第二个解 {$\text{Tree}(a)_2$}，在很多介绍 ADT 的材料中就被选择性无视了……[9] 在介绍 Catalan Numbers 的母函数（Generating Function）时也遇到了这个解。

以上的内容从母函数的角度也可以进行很好的诠释。

[9] 中给出的解释是，由于我们已经知道 {$\text{Tree}(0) = 1$}，所以把 {$0$} 代入 {$\text{Tree}(a)_1$} 和 {$\text{Tree}(a)_2$} 检查是否会得到 {$1$}。然而对于两个解来说，{$a = 0$} 都会导致分母为 {$0$} 的情况。{$\text{Tree}(a)_1$} 是 {$0/0$} 型，所以用洛必达法则可以验证。{$\text{Tree}(a)_2$} 则很不幸地不满足洛必达法则的使用条件，抢救的机会都没有了……

到目前为止的内容似乎都没有体现出很明显的实际作用。下一次会提到通过对一个 ADT 的代数表达式求导，可以得到该 ADT 的 one-hole context [3]，从而方便地在在数据结构上移动焦点并显著降低不可变数据结构的更新成本。